Retime a path subject to robust kinematic constraints

import toppra as ta
import toppra.constraint as constraint
import toppra.algorithm as algo
import numpy as np
import matplotlib.pyplot as plt
import argparse


parser = argparse.ArgumentParser(
    description="An example showcasing the usage of robust constraints."
    "A velocity constraint and a robust acceleration constraint"
    "are considered in this script."
)
parser.add_argument(
    "-N",
    "--N",
    type=int,
    help="Number of segments in the discretization.",
    default=100,
)
parser.add_argument("-v", "--verbose", action="store_true", default=False)
parser.add_argument("-du", "--du", default=1e-3, type=float)
parser.add_argument("-dx", "--dx", default=5e-2, type=float)
parser.add_argument("-dc", "--dc", default=9e-3, type=float)
parser.add_argument("-so", "--solver_wrapper", default="ecos")
parser.add_argument("-i", "--interpolation_scheme", default=1, type=int)
args = parser.parse_args()
if args.verbose:
    ta.setup_logging("DEBUG")
else:
    ta.setup_logging("INFO")

# Parameters
N_samples = 5
dof = 7

# Random waypoints used to obtain a random geometric path.
np.random.seed(9)
way_pts = np.random.randn(N_samples, dof)

# Create velocity bounds, then velocity constraint object
vlim_ = np.random.rand(dof) * 20
vlim = np.vstack((-vlim_, vlim_)).T
# Create acceleration bounds, then acceleration constraint object
alim_ = np.random.rand(dof) * 2
alim = np.vstack((-alim_, alim_)).T

path = ta.SplineInterpolator(np.linspace(0, 1, 5), way_pts)
pc_vel = constraint.JointVelocityConstraint(vlim)
pc_acc = constraint.JointAccelerationConstraint(
    alim, discretization_scheme=constraint.DiscretizationType.Interpolation
)
robust_pc_acc = constraint.RobustLinearConstraint(
    pc_acc, [args.du, args.dx, args.dc], args.interpolation_scheme
)
instance = algo.TOPPRA(
    [pc_vel, robust_pc_acc],
    path,
    gridpoints=np.linspace(0, 1, args.N + 1),
    solver_wrapper=args.solver_wrapper,
)

X = instance.compute_feasible_sets()
K = instance.compute_controllable_sets(0, 0)

_, sd_vec, _ = instance.compute_parameterization(0, 0)

X = np.sqrt(X)
K = np.sqrt(K)

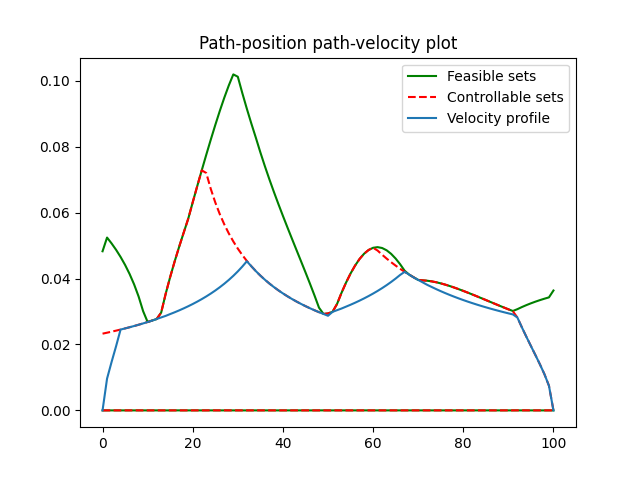
plt.plot(X[:, 0], c="green", label="Feasible sets")
plt.plot(X[:, 1], c="green")
plt.plot(K[:, 0], "--", c="red", label="Controllable sets")
plt.plot(K[:, 1], "--", c="red")
plt.plot(sd_vec, label="Velocity profile")
plt.legend()
plt.title("Path-position path-velocity plot")
plt.show()

jnt_traj = instance.compute_trajectory(0, 0)
ts_sample = np.linspace(0, jnt_traj.duration, 100)
qs_sample = jnt_traj.evaldd(ts_sample)

plt.plot(ts_sample, qs_sample)
plt.show()

Out:

INFO [algorithm.py : 191] Successfully parametrize path. Duration: 37.417, previously 1.000)
INFO [algorithm.py : 193] Finish parametrization in 1.927 secs